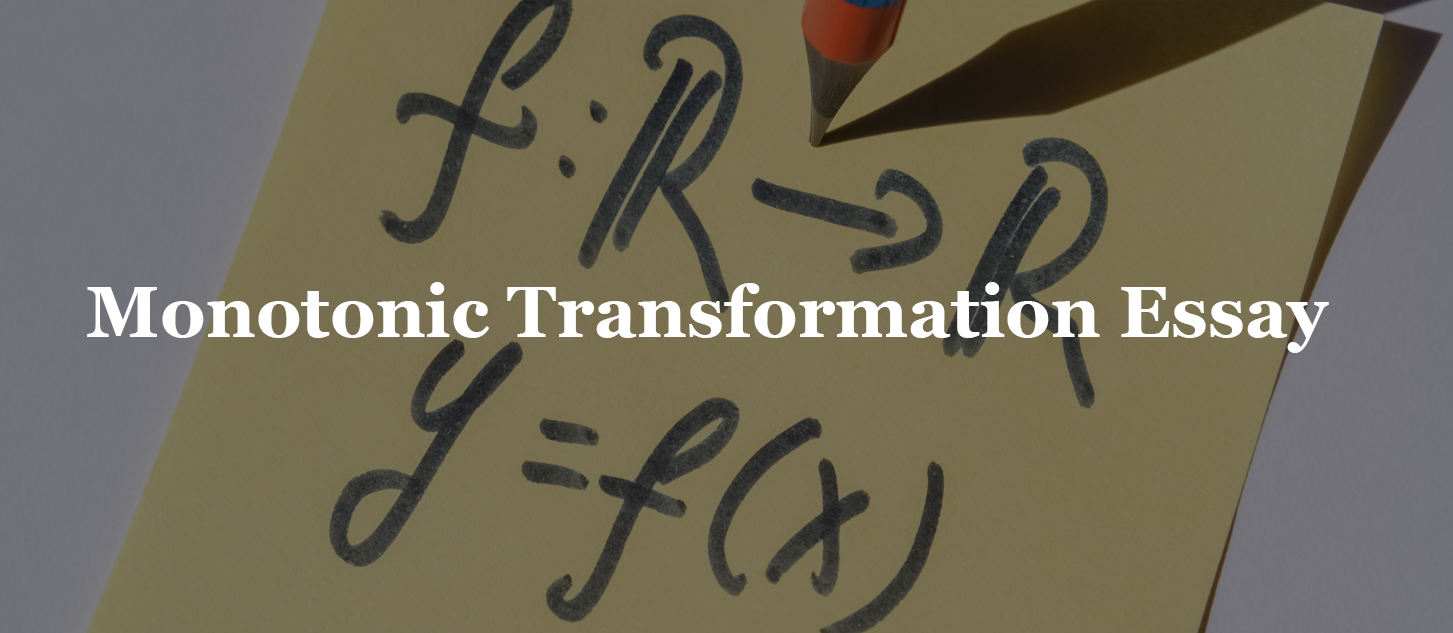The monotonic transformation is a simple method of transforming a set of numbers into another set of a number without disturbing the originality of the numbers. It means that the identity of the numbers remain the same and there is no change in the identity of numbers. Similarly, the order in which the numbers are present in a particular set remains the same.
In simple words, it is easy to understand that a function is monotonic when it changes real numbers into real numbers and vice versa. If we talk about monotonic transformation in terms of mathematics, then it is easy to say that a function is monotonic when it completely satisfies the property when x>y, then f(x)>f(y).
The mathematical property shows that a monotonic function has increasing property. It is a positive transformation and it has nothing to do with the sign on the function,
Example of monotonic transformation
For instance, the original utility function is U(x,y), then it is very easy for us to represent the monotonic transformation by fUxy [ ( , )]. Here, f[.] is the property of the function and it is actually responsible for making it a monotonic function.
Monotonic function
We can say that a function is a monotonic function if it has an identical trend. This means that either the function is not increasing or the function is not decreasing. In simple words, we can say that the function is identical. There is no special change in the function over time.
Likewise, another sign of the monotonic function is that the first derivative of the function has no impact on the sign of function. Commonly, the sign of a function changes after the first derivative. It means the positive sign of the function changes into negative and vice versa.
However, it is not the case for monotonic function as the sign does not change and the function remains the same. However, it is essential to keep it in mind that it is not necessary for a function to be continuous. The first derivative of the function can either continuous or not but it has no effect on the sign of the function.
Common examples of monotonic functions
Some of the common examples of the monotonic functions are
F(U) = 2U
function(U) = 3U
f(U) = U+2
fun(U) = U+10
F(U) = 5+3U
(U) = U3
Tests for a monotonic function
Two types of tests are available for monotonic functions. These tests help to understand the trend of a monotonic function. It means that a function may increase or decrease depending upon this test.
For instance, we can suppose that a function is continuous on [a, b]. At the same time, the function is differential on (a, b). The derivative of the function can help us in this regard to determine whether the function is positive or negative.
For the first condition, take the derivative of the function and if it is larger than zero for all x in (a, b). It means that the function is increasing on [a, b]. On the other hand, take the derivative of the function and if it is less than zero for all x in (a, b) it means that the function is decreasing on [a, b].
This test can help to understand that a function is monotonic or not because a monotonic function is no increase and no decreasing and it remains constant and the sign of the function also remains same after the first derivative.
Utility function
It is important to have a brief overview of the utility function, as it is the most critical function in case of monotonic transformation. A utility function is a mathematical function that helps to rank alternatives to their respective utility for an individual.
Reflection of the utility function
It is essential to understand the reflection of a utility function to determine the actual meaning of the function or to understand what it means. Apart from the mathematical justification, utility function has a proper role in economics and it relates to the concept that helps to determine the preferences over a certain set of goods and services.
Utility function helps to measure and to find these preferences over set of goods and services in proper order. A special unit is required to measure this function and it is known as utils. The unit helps to understand the satisfaction level of the customers about certain goods and services they are consuming.
Method to calculate utility function
The first step to calculate a utility function is to determine MU. The next step in this context is to divide the difference for overall utility by the total difference present in the units. The marginal cost of a certain good or service is obtained in this context by dividing these. It reflects the cost of the extra units consumed in this process.
Monotonic transformation for a utility function
It is good to understand the monotonic transformation for a utility function in economics. The monotonic transformation for a utility function is actually a utility function that helps to understand similar preferences. It means that the transformed monotonic utility function gives an understanding of the original utility function. It means that there is no change in bundles or the ranking of the function when there is monotonic transformation.